Algorithmes de tri – algorithmes lents­­

­

Salut les internautes. Aujourd’hui, nous allons parler du tri. « Inutile » ? « Evident » ? Pas tant que ça. Revoyons un peu les algorithmes de tri et leurs particularités. Ce que nous appelons “algorithmes de tri” sont des algorithmes utilisés pour trier les éléments d’un tableau. Ils sont communément utilisés dans les programmes informatiques (Excel ou bases de données par exemple). Dans cet article, nous appelons n la taille du tableau à trier. Cet article traite des algorithmes lents (complexité en O(n²)). Si vous n’avez aucune idée de ce qu’est la complexité, vous pouvez jeter un coup d’œil à mon billet à ce sujet. Je vais écrire deux autres articles pour examiner les algorithmes efficaces (O(n·log(n)) et un dernier pour présenter des algorithmes spéciaux permettant de trier des tableaux d’un type particulier en temps linéaire.

Le tri par insertion

Le premier algorithme de tri est le tri par insertion. L’idée de base est de faire trier une partie du tableau, et chaque élément qui n’est pas trié est inséré à sa place. La complexité de cet algorithme est quadratique. En effet, pour chaque élément, il est nécessaire de rechercher dans la partie triée du tableau la position du nouvel élément. Cette partie triée peut être arbitrairement grande (mais toujours plus petite que n). Parce que nous devons faire une telle chose pour chaque élément. La complexité est donc en O(n²). La figure suivante montre comment l’algorithme fonctionne.

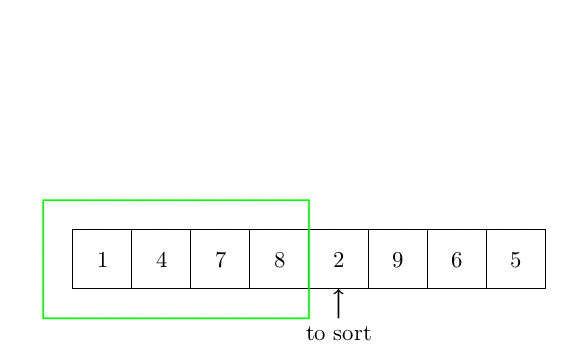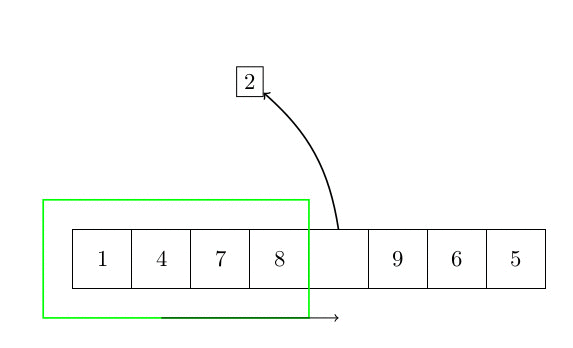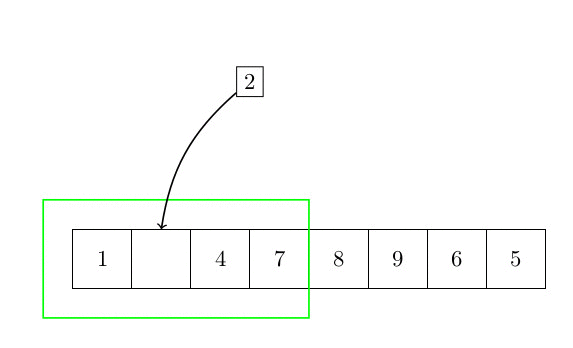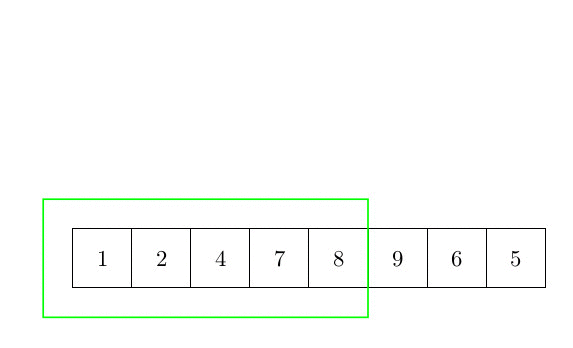
Plus formellement, l’algorithme peut s’écrire :

Insertion_sort(t):
  for i ← 1 to n
    j ← i
    while j > 0 and t[j-1] > t[j]
      t[j] ↔ t[j-1]
      j ← j - 1
    end while
  end for
end

Dans le pire des cas, chaque boucle de temps fera i échanges. La complexité est donc en ==O(n²).

Le tri par sélection

Cet algorithme de tri n’est pas plus compliqué que le tri par insertion. Le principe est le suivant. On recherche le plus petit élément et on l’échange avec le premier élément du tableau, puis on le considère comme trié. Ensuite, et jusqu’à ce qu’il ne reste plus aucun élément non trié, on recherche le plus petit élément dans la partie non triée du tableau et on sélectionne le plus petit élément. On l’échange avec le premier élément de la partie non triée du tableau et on le considère comme trié. La figure suivante donne une idée du tri d’un élément du tableau (la partie verte du tableau est déjà triée). La complexité est quadratique, car il faut rechercher le min de la partie restante du tableau (complexité n) pour chaque élément (n fois)

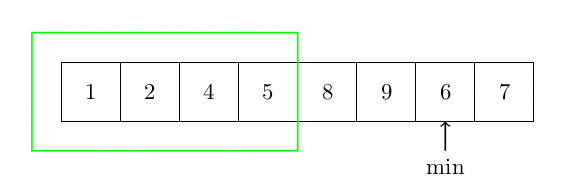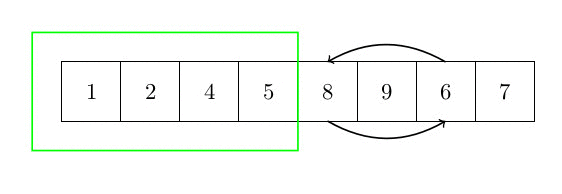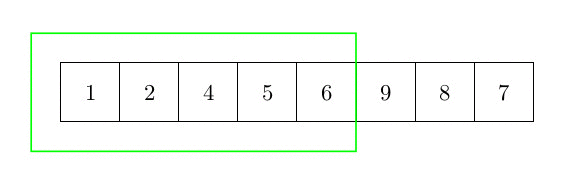
Plus formellement, l’algorithme peut s’écrire :

selection_sort(t):
  for j ← 0 to n
    i_min ← t[j]
    for i ← j+1 to n
      if(t[i]<t[i_min])
        i_min ← i
      end if
    end for
    if i_min ≠ j
      t[i_min] ↔ t[j]
    end if
  end for
end

L’analyse de la complexité est aussi simple que l’analyse du type d’insertion. Pour chaque i, il est nécessaire d’examiner les éléments (n – i) afin de trouver le min. La complexité est donc therefore= =O(n²).

Le tri à bulles

Le dernier algorithme de tri que nous analyserons dans cet article est le tri à bulles. Le tri à bulles est très différent des deux autres, car il déplace les éléments beaucoup plus souvent. L’idée principale du tri à bulles est d’ordonner les éléments par paires lorsque vous les comparez. Le tri à bulles prend les éléments du début du tableau et les compare par paires : le premier est comparé au second, et s’il est plus grand, les deux éléments sont échangés. Ensuite, le deuxième est comparé au troisième, etc. L’élément le plus grand est donc correctement ordonné à la fin de la première boucle. Ensuite, le processus est répété jusqu’à ce qu’il n’y ait plus d’échange. La complexité de cet algorithme est un peu plus grande que les autres et sera analysée après l’algorithme. La figure ci-dessous représente une étape de cet algorithme :

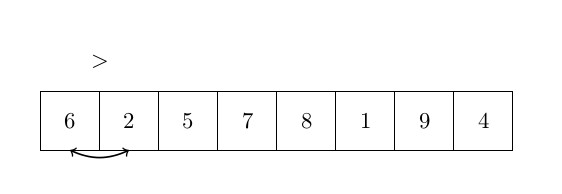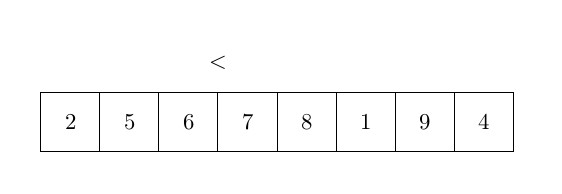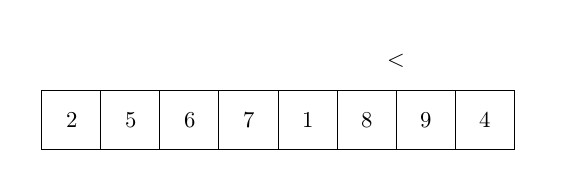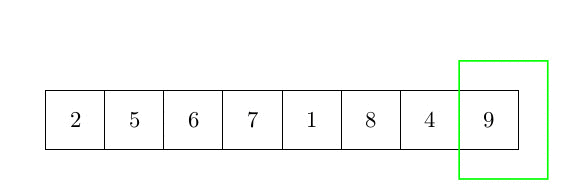
et l’algorithme peut s’écrit :

bubble_sort(t):
  swapped ← true
  while swapped
     swapped ← false
     for i ← 1 to n-1
       if t[i-1] > t[i]
         t[i-1] ↔ t[i]
         swapped ← true
       end if
     end for
   end while
end

Chaque boucle de la boucle “while” met en place un élément à l’extrémité du tableau non trié. La boucle while est donc exécutée au maximum n fois. Pour chaque boucle while, n – 1 comparaisons sont effectuées. La complexité est donc n² – n=O(n²).

C’est tout ! Il manque un algorithme de complexité quadratique, le meilleur, le Quick Sort. Mais comme son nom l’indique, ce tri est très efficace en moyenne, et sera donc analysé avec les tris efficaces dans le prochain article sur le tri. D’ici-là, renseignez-vous, réfléchissez et surtout, n’oubliez pas de rêver !