Salut les internautes. Dans le premier billet de cette série, nous avons parlé du tri, et plus précisément des algorithmes lents (complexité de ![]() dans le pire des cas). Aujourd’hui, nous allons aborder trois sujets (oui, vous avez de la chance) : nous présentons deux algorithmes dont la complexité est de
dans le pire des cas). Aujourd’hui, nous allons aborder trois sujets (oui, vous avez de la chance) : nous présentons deux algorithmes dont la complexité est de ![]() , un algorithme “lent” dans le pire des cas (
, un algorithme “lent” dans le pire des cas (![]() ) mais qui est efficace et vraiment rapide en moyenne et enfin une démonstration selon laquelle les algorithmes de tri qui comparent des éléments ne peuvent pas avoir une complexité meilleure que
) mais qui est efficace et vraiment rapide en moyenne et enfin une démonstration selon laquelle les algorithmes de tri qui comparent des éléments ne peuvent pas avoir une complexité meilleure que ![]() . Rappelons que nous voulons trier un tableau
. Rappelons que nous voulons trier un tableau ![]() de taille
de taille ![]() .
.
Le tri rapide (ou quicksort)
OK, commençons par le tri rapide. Le tri rapide est un « algorithme lent » en ce sens que sa complexité dans le pire des cas est de ![]() . Cependant, la complexité moyenne est de
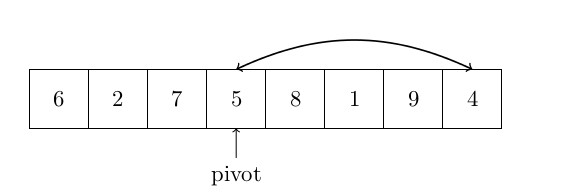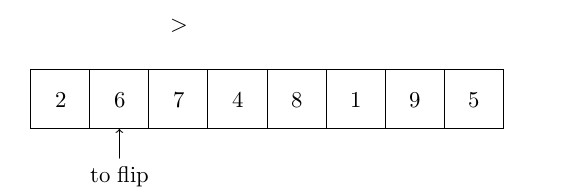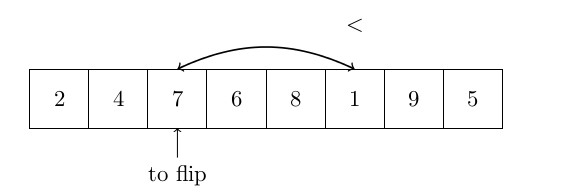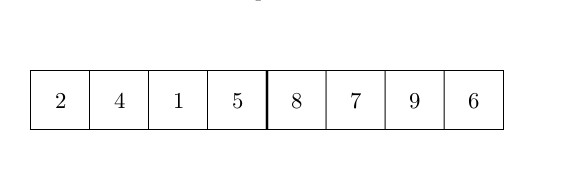
. Cependant, la complexité moyenne est de ![]() . De plus, ce type d’algorithme est largement utilisé dans de nombreux logiciels (Excel par exemple) et nous avons donc décidé de le mettre ici. Le quicksort fonctionne comme suit : un pivot est choisi parmi les éléments (c’est l’un des points clés de cet algorithme) et est placé en fin de tableau. Ensuite, tous les éléments sont comparés à ce pivot. Tous les éléments plus petits que le pivot sont mis “au début” du tableau, les autres éléments (plus grands) sont laissés à leur place (“à la fin” du tableau). Les petits éléments sont mis “au début” en utilisant un index pour échanger les points sur le premier grand élément, et qui sera retourné avec le plus petit élément trouvé. Cet index est ensuite incrémenté. Le quicksort s’exécute alors sur tous les sous-ensembles des éléments plus petits que le pivot et une seconde fois sur les éléments plus grands que le pivot. La figure ci-dessous montre comment l’algorithme fonctionne :
. De plus, ce type d’algorithme est largement utilisé dans de nombreux logiciels (Excel par exemple) et nous avons donc décidé de le mettre ici. Le quicksort fonctionne comme suit : un pivot est choisi parmi les éléments (c’est l’un des points clés de cet algorithme) et est placé en fin de tableau. Ensuite, tous les éléments sont comparés à ce pivot. Tous les éléments plus petits que le pivot sont mis “au début” du tableau, les autres éléments (plus grands) sont laissés à leur place (“à la fin” du tableau). Les petits éléments sont mis “au début” en utilisant un index pour échanger les points sur le premier grand élément, et qui sera retourné avec le plus petit élément trouvé. Cet index est ensuite incrémenté. Le quicksort s’exécute alors sur tous les sous-ensembles des éléments plus petits que le pivot et une seconde fois sur les éléments plus grands que le pivot. La figure ci-dessous montre comment l’algorithme fonctionne :
Voici l’algorithme formel:
quicksort(t, a, b):
if a < b:
p ← partition(A, a, b)
quicksort(A, a, p-1)
quicksort(A, p+1, b)
end if
end
La condition if est utilisée pour voir s’il y a un élément unique (le premier élément est aussi le dernier). Maintenant, regardons la fonction de partition :
partition(t, a, b):
pivot ← pivot(t)
to_flip ← a
for i ← a to b-1:
if t[i] ≤ pivot:
t[to_flip] ↔ t[i]
to_flip ← to_flip+1
end if
end for
t[to_flip] ↔ t[b]
return to_flip
end
Notons l’utilisation de la fonction pivot. Cette fonction est le premier, le dernier élément, ou encore l’élément du milieu, soit une heuristique pour trouver un élément pertinent.
Cette fonction est très importante pour analyser la complexité de cet algorithme. En effet, si le pivot n’est pas correctement choisi, tous les éléments seront plus grands (ou plus petits), ce qui conduit à une équation de complexité :
![]()
et donc une complexité de ![]() . Cependant, et s’il y a un
. Cependant, et s’il y a un ![]() tel qu’au moins
tel qu’au moins ![]() éléments sont plus petits que le pivot et au moins
éléments sont plus petits que le pivot et au moins ![]() éléments sont également plus grands que le pivot, alors nous obtenons l’équation de complexité :
éléments sont également plus grands que le pivot, alors nous obtenons l’équation de complexité :
![]()
Dans ce cas, on obtient une complexité de ![]() . Ici, j’analyse la complexité dans le cas où
. Ici, j’analyse la complexité dans le cas où ![]() . Dans ce cas, nous avons :
. Dans ce cas, nous avons :
![]()
Dans ce cas, le théorème du maître nous donne ![]() . Malgré la complexité dans le pire des cas, la complexité moyenne dans la plupart des cas est asymptotiquement aussi bonne que les deux autres algorithmes que nous présentons. De plus, les constantes de cette complexité sont assez faibles, et le temps nécessaire pour effectuer le calcul est assez court. Enfin, l’algorithme trie “en place”, ce qui est avantageux en termes de mémoire.
. Malgré la complexité dans le pire des cas, la complexité moyenne dans la plupart des cas est asymptotiquement aussi bonne que les deux autres algorithmes que nous présentons. De plus, les constantes de cette complexité sont assez faibles, et le temps nécessaire pour effectuer le calcul est assez court. Enfin, l’algorithme trie “en place”, ce qui est avantageux en termes de mémoire.
Le tri fusion
Maintenant, examinons un type de comparaison vraiment asymptotiquement efficace, le type de fusion. Le principe du tri fusion consiste à diviser le tableau en deux parties de longueur égale, à les trier de manière récursive, puis à fusionner ces deux sous-tableaux. Pour ce faire, les deux plus petits éléments des sous-réseaux sont comparés et le plus petit est placé dans le tableau final et retiré du sous-réseau correspondant. La fusion se poursuit de cette manière jusqu’à ce qu’il ne reste plus aucun élément dans les sous-réseaux. L’image ci-dessous montre comment l’algorithme fonctionne :

Voici l’algorithme formel :
merge_sort(t, a, b):
if t.length>1:
return merge(merge_sort(t, a, (a+b)/2), merge_sort(t, a, (a+b)/2)
end if
end
Cet algorithme nécessite une fonction auxiliaire qui fusionne les deux sous-listes dans un tableau trié :
merge(t1, t2):
if isempty(t1)
return t2
else if isempty(t2)
return t1
else if t1[1]>t2[1]
return [t2[1],merge(t1, t2[2,…])]
else
return [t1[1],merge(t1[2,…], t2)]
end if
end
Nous utilisons la notation t[2,…] pour le tableau contenant tous les éléments de t sauf le premier, et [a, t] pour le tableau composé de a suivi par les éléments de t.
Maintenant, parlons de la complexité. Eh bien, c’est assez simple, le tableau est divisé en deux parties, et ensuite, afin de fusionner les sous-tableaux, chaque élément est analysé une fois. Par conséquent, la complexité globale peut être exprimée par l’équation suivante :
![]()
ce qui résulte, selon le théorème de Master, en une complexité de ![]() .
.
Tri par tas
Le tri par tas repose sur une façon inhabituelle de représenter les données : avec un tas. Le tableau est donc conceptuellement la représentation d’un tas binaire avec la propriété suivante : pour chaque nombre ![]() , on considère deux sous-tas :
, on considère deux sous-tas : ![]() et
et ![]() .
.
La première étape de l’algorithme consistera à faire respecter la règle de base du tas : le père de deux nœuds doit être plus grand que ses enfants. Pour ce faire, nous analysons tous les éléments. Lorsqu’un élément ![]() est plus grand que son père, ils sont échangés, et
est plus grand que son père, ils sont échangés, et ![]() est comparé avec son nouveau père, jusqu’à ce qu’il soit plus petit que son père (ou qu’il soit la racine du tas). À la fin de cette première étape, l’élément le plus grand est à la racine du tas. Il est alors possible de l’échanger avec le dernier élément, et de le considérer en dehors du tas.
est comparé avec son nouveau père, jusqu’à ce qu’il soit plus petit que son père (ou qu’il soit la racine du tas). À la fin de cette première étape, l’élément le plus grand est à la racine du tas. Il est alors possible de l’échanger avec le dernier élément, et de le considérer en dehors du tas.
La racine du tas est maintenant l’élément qui était auparavant le dernier élément. Nous répétons ensuite l’algorithme qui fait de l’arbre un tas. Le deuxième plus grand élément du tableau est maintenant la tête du tas. Il est échangé avec le dernier élément du tas, qui est l’avant-dernier élément du tableau. Ce processus est répété jusqu’à ce qu’il n’y ait plus d’élément dans le tas. La figure suivante illustre le fonctionnement de l’algorithme.
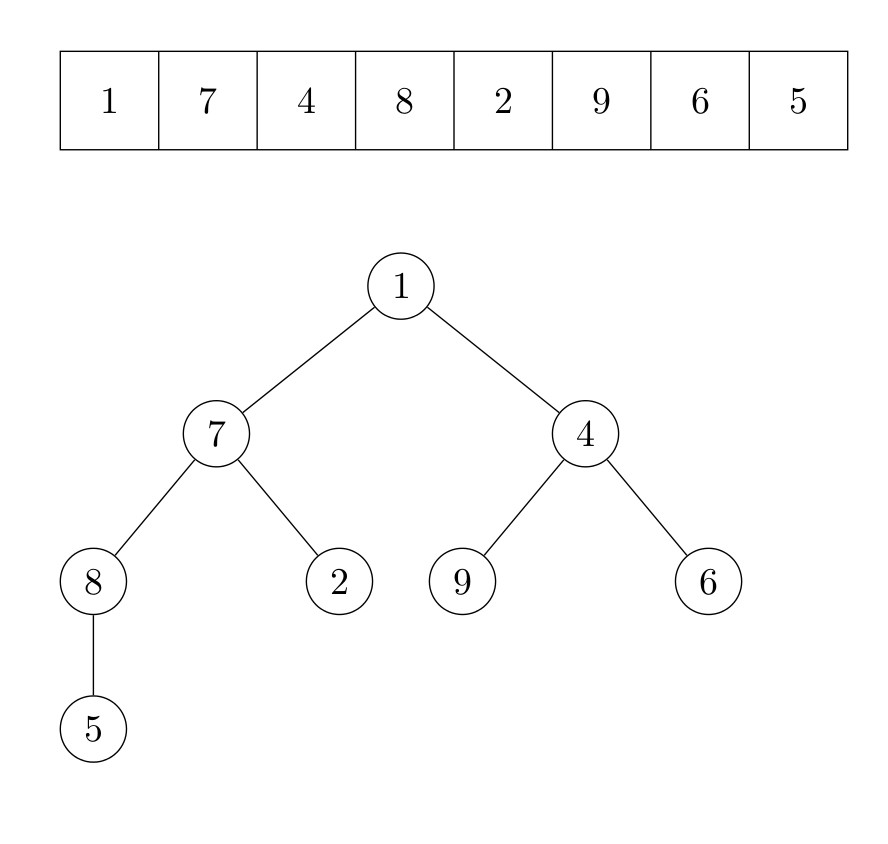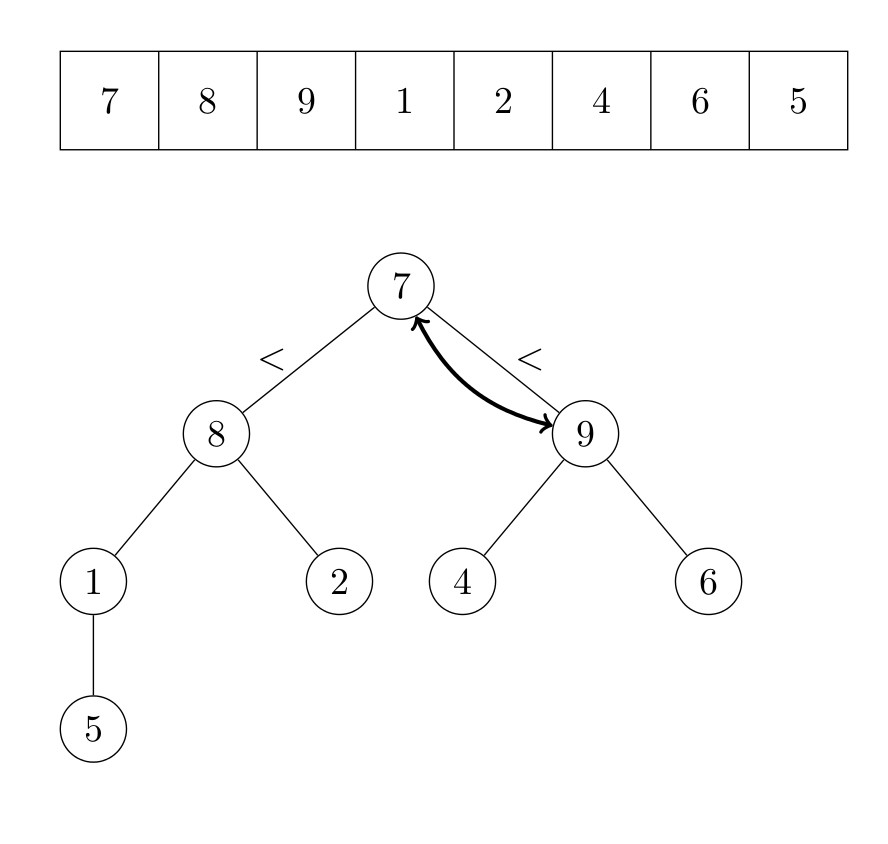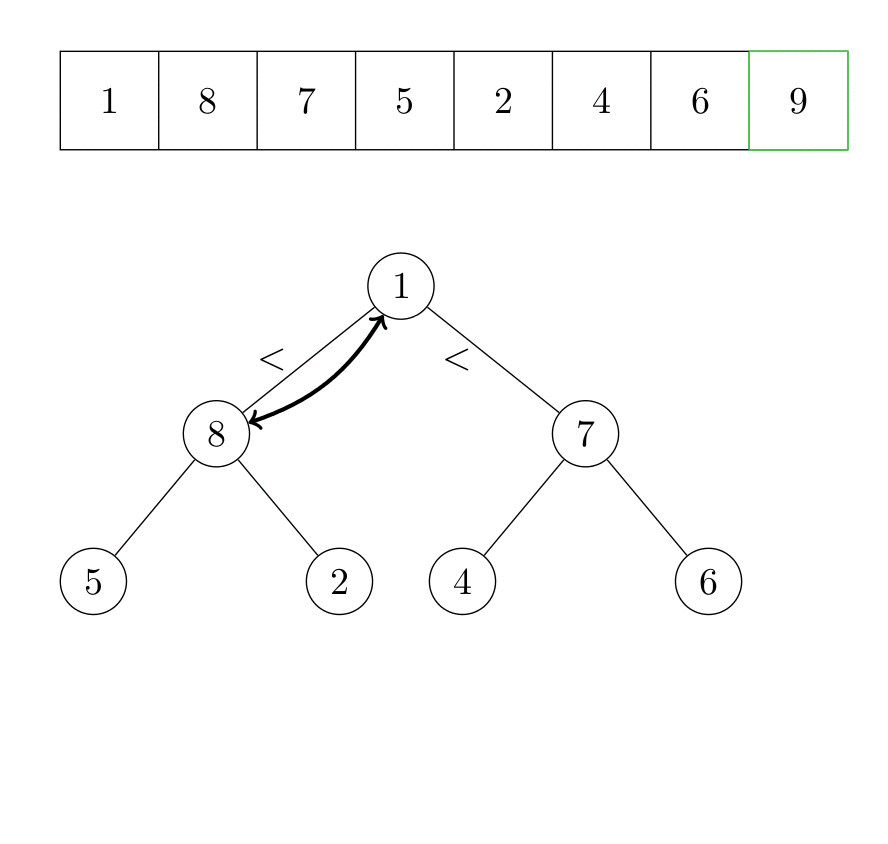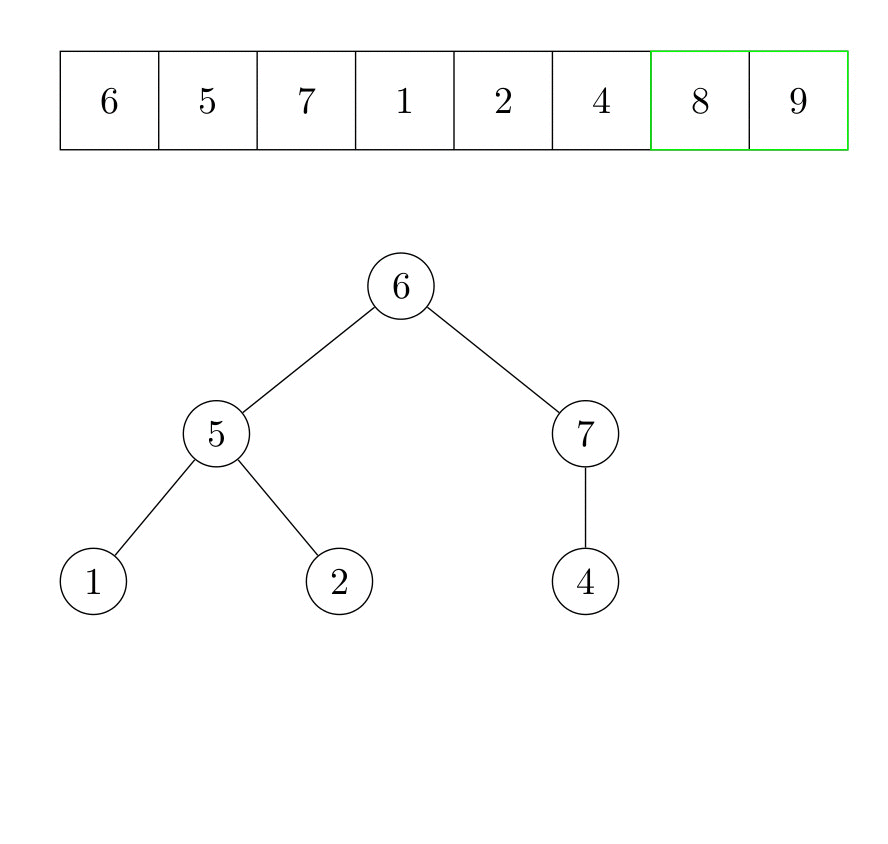
Formellement, l’algorithme s’écrit :
heapsort(t):
for i ← n/2 to 1
heapify(t, i, n)
end for
for i ← n to 2
t[i] ↔ t[1]
heapify(t, 1, i-1)
end for
end
et la fonction auxiliaire heapify, qui assure le respect de la règle du tas :
heapify(t, node, length):
k ← nœud
j ← 2k
while j ≤ n:
if j < n and t[j] < t[j+1]
j ← j+1
end if
if t[k] < t[j]
t[k]↔t[j]
k ← j
j ← 2k
else
end
end if
end while
end
Analysons la complexité de cet algorithme. La première étape de l’algorithme prend ![]() . La deuxième partie de l’algorithme peut être analysée de cette manière. Le tas est de
. La deuxième partie de l’algorithme peut être analysée de cette manière. Le tas est de ![]() de haut. Il y a alors au maximum
de haut. Il y a alors au maximum ![]() inversions, pour chaque tas, et
inversions, pour chaque tas, et ![]() tas. La complexité est alors de
tas. La complexité est alors de ![]() .
.
Une limite sur la complexité des tris par comparaison
La dernière partie de cet article vise à analyser la complexité optimale des algorithmes de tri en utilisant la comparaison comme principe de base. Nous prouvons que la complexité optimale pour ces algorithmes est de ![]() .
.
Le but d’un tri par comparaison est de faire un certain nombre de comparaisons (comparer les éléments 2 par 2) afin de les ordonner. Il est possible de représenter ces sortes dans un arbre binaire. Ce type d’arbre est appelé arbre de décision. Chaque feuille de l’arbre correspond à un tri potentiel particulier (une permutation) du tableau. Il existe ![]() permutations possibles d’éléments.1. La complexité dans le pire des cas est donc la hauteur d’un arbre avec des feuilles de
permutations possibles d’éléments.1. La complexité dans le pire des cas est donc la hauteur d’un arbre avec des feuilles de ![]() , ce qui donne :
, ce qui donne : ![]() . Nous utilisons le
. Nous utilisons le ![]() de chaque côté et nous utilisons ensuite l’approximation de Stirling2, nous obtenons :
de chaque côté et nous utilisons ensuite l’approximation de Stirling2, nous obtenons : ![]() .
.
Nous avons donc maintenant montré quelque chose d’assez important sur les tris. Mais cela ne concerne que les algorithmes utilisant la comparaison. La prochaine fois, nous verrons qu’en utilisant des types de données particuliers, il est possible d’éviter d’utiliser la comparaison et d’obtenir une complexité linéaire. D’ici-là, renseignez-vous, réfléchissez et surtout n’oubliez pas de rêver.