Algorithmes de tri – algorithmes en temps linéaire

Salut les internautes. Aujourd’hui, nous concluons la série de billets sur les algorithmes de tri (le premier sur les algorithmes lents est ici, et le second sur les algorithmes efficaces est ici) par un billet sur les algorithmes de temps linéaire. Ces algorithmes sont moins connus que les précédents, et pour une bonne raison. Pour trier en temps linéaire, il est nécessaire d’imposer des contraintes sur les données d’entrée. Cependant, ces algorithmes de tri peuvent être très utiles dans des situations particulières. Rappelons l’objectif des algorithmes de tri : nous voulons trier un tableau $t$ d’éléments $n$ .

Tri comptage

Parlons d’abord du tri de comptage. Il y a deux contraintes à ce tri. La première est que les données doivent être entières. La seconde est que l’élément le plus grand doit être du même ordre que la taille du tableau. Le tri par comptage fonctionne comme suit :

D’abord, on crée un tableau auxiliaire $aux$ . La taille de ce tableau est le plus grand élément de $t$ . On initialise chaque élément de ce tableau avec une valeur 0.
Ensuite, on parcourt $t$ , et pour chaque $t[i]$ , on augmente $aux[t[i]]$ de un. À la fin de ce processus, chaque élément du tableau auxiliaire contiendra le numéro de l’élément correspondant en $t$ . Par exemple, s’il y a 3 fois la valeur 0 dans $t$ , alors $aux[0]$ contiendra 3.
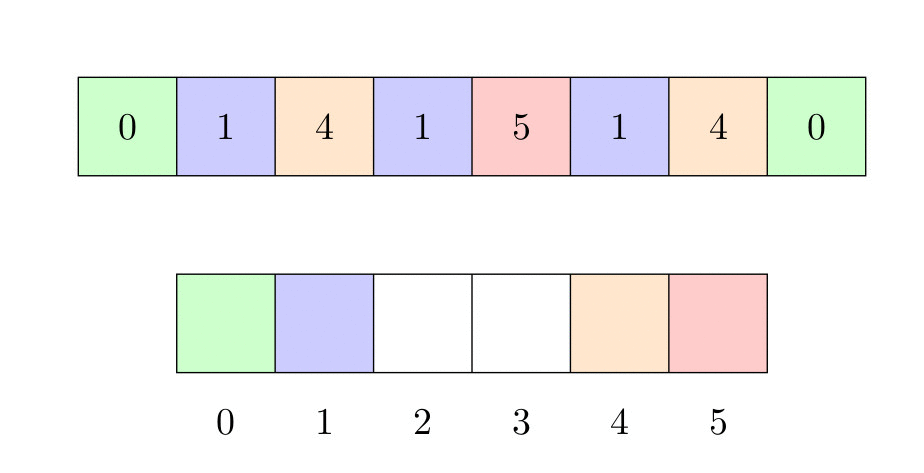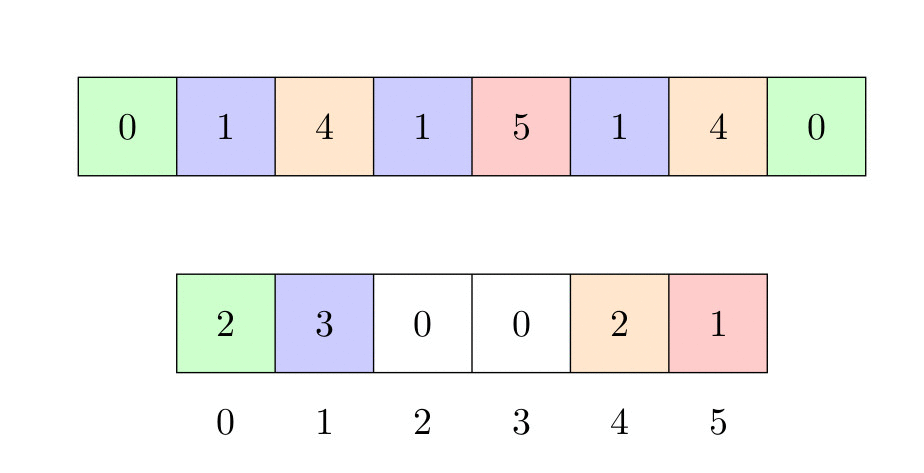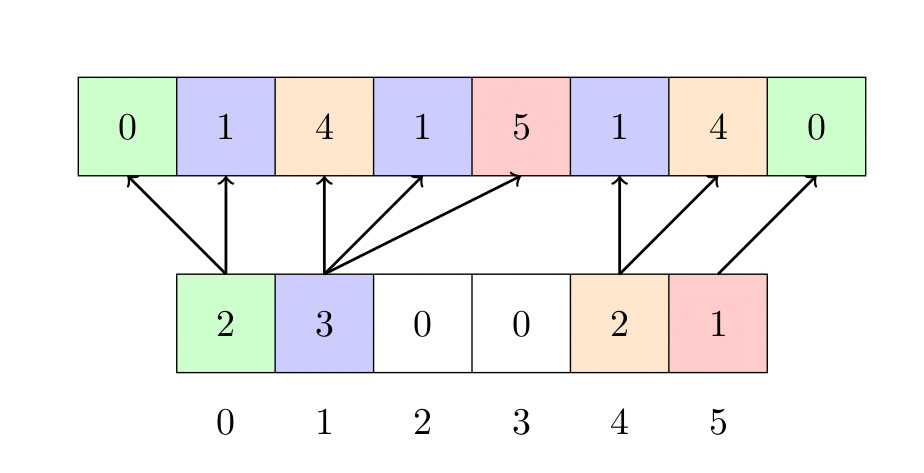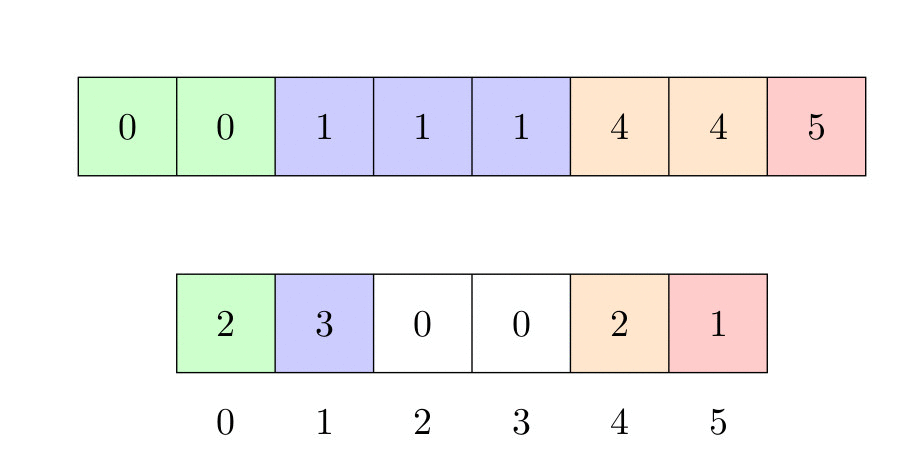
L’objectif de la troisième étape est de remplacer le nombre d’occurrences de chaque élément du tableau auxiliaire par la position du dernier élément de cette valeur dans le tableau final. Cette étape peut sembler inutile, mais nous verrons plus tard que l’une des propriétés les plus importantes de ce tri est qu’il est stable, ce qui signifie que si vous triez effectivement les clés des éléments, l’ordre des éléments ayant des clés similaires sera préservé.
Enfin, on place les éléments dans un nouveau tableau (si nous trions effectivement les clés) ou dans le même tableau (autrement). Pour ce faire, on place les éléments en prenant le dernier élément de a et en le plaçant au bon endroit, en regardant dans le tableau. Le tableau auxiliaire est diminué de manière cohérente.

L’image ci-dessous montre comment le tri fonctionne :

L’algorithme formel est :

counting_sort:
  k←max(t) 
  aux←integer[k]
  for i←0 to k
    aux[i]←0
  end for
  for j←1 to n
    aux[t[j]]←aux[t[j]]+1
  end for
  final←integer[n]
  for i←n to 1
    final[aux[t[j]]]←t[j]
    aux[t[j]]←aux[t[j]]-1
  end for
  return final
end

La complexité est de $O(n+k)$ (parce que max a une complexité de $n$ ). Comme $O(k) = O(n)$ , la complexité globale est de $O(n)$ .

Le tri radix

Le tri radix est assez simple, mais il nécessite un tri stable pour les éléments entiers. Les contraintes sur les données d’entrée sont que les éléments sont entiers et que le nombre de chiffres pour chaque nombre est très petit ( $O(1)$ ). Le tri radix utilise l’algorithme de tri pour trier les éléments (entiers), chiffre par chiffre. Il commence par le dernier chiffre (le moins significatif). Pourquoi ? Il est nécessaire de trier d’abord sur les derniers éléments car un tri sur un chiffre écrasera le précédent. Cependant, et comme l’algorithme de tri est stable, le fait de trier deux éléments qui ont le même chiffre à la position $i$ ne changera pas le tri sur les chiffres précédents.

L’animation suivante montre comment fonctionne le tri radix :

L’algorithme est très simple :

radix_sort:
  k←nb_digit(max(t))
  for j←k to 1
    t←stable_sort(t, jth digit)
  end for
end

où stable_sort(t, key)est un tri stable du tableau t, sur la clé key. La complexité dépend totalement de l’algorithme de tri utilisé à l’intérieur. En particulier, l’utilisation du tri par comptage conduit à une complexité linéaire ( $O(n)$ ).

Le tri par packets

Le tri par paquets est également assez simple, mais il a une hypothèse très forte. Les éléments sont censés être “bien répartis” entre 0 et 1, ce qui signifie qu’il correspond à une distribution aléatoire. Le tri par paquets fonctionne comme suit : l’intervalle $[0,1]$ est divisé en parties de $n$ , appelées paquets. Comme les éléments sont bien répartis, il y a des éléments $O(1)$ dans chacun de ces intervalles. Un tri par comparaison est ensuite utilisé sur chacun des paquets, de complexité $O(1)$ . La complexité globale est alors de $n\cdot O(1)=O(n)$ . L’algorithme formel est :

bucket_sort:
  aux←list[]
  for i←0 to n-1
    aux[i]←[]
  end for
  for i←1 to n
    aux[floor(n*t[i])]←concat(aux[floor(n*t[i])],t[i])
  end for
  for i←0 to n-1
    sort(aux[i])
  end for
  final←float[]
  for i←0 to n-1
    final←concat(final,aux[i])
  end for
  return final
end

Le principe de l’algorithme est assez simple, et observer son déroulement n’aide pas vraiment, donc je ne mettrai aucune illustration pour cet algorithme.

C’est le tout dernier algorithme de tri que je voulais vous présenter. Il y en a d’autres en effet, mais la plupart sont des variantes de ceux que j’ai présentés. J’espère que cet article pourra vous aider si vous avez besoin de mettre en œuvre un algorithme de tri, et de choisir largement parmi tous les algorithmes que j’ai présentés. Les prochains articles sur les algorithmes porteront sur d’autres sujets. D’ici-là, renseignez-vous, réfléchissez et surtout n’oubliez pas de rêver.

Tri comptage

Le tri radix

Le tri par packets

Cédric Buron

Laisser un commentaire Annuler la réponse